Quantum Kernels

The quantum version of SVM was initially proposed by Rebentrost et al. (2014), but this formulation requires the input data to be provided in coherent superposition states. Therefore, when the data are generated on a classical computer, the efficient application of this approach becomes impractical. 

A different approach was proposed by Havlíček et al. (2019), where the data are provided purely classically, while the feature space is mapped by the quantum state $ \Phi: \mathbb{R}^n \rightarrow \vert \Phi(\vec{x}) \rangle \langle \Phi(\vec{x}) \vert $.

A commonly used feature map is ZZFeatureMap, this is a module of qiskit library, which involves a non-linear mapping of the input features. The encoding process works as follows: 

• Initial State: The process begins by preparing all qubits in the initial state $ \vert 0^{\otimes n} \rangle $, followed by the application of Hadamard gates to create a uniform superposition.
• Single-Qubit Rotations: The classical data points are encoded into the rotation angles of single-qubit phase gates.
• Two-Qubit Entanglement/Rotations: Entangling layers, typically using CNOT gates, are applied between specified pairs of qubits to introduce two-qubit interactions.

The following equation describes the ZZFeatureMap: \begin{equation*} \mathcal{U}_{\Phi(\vec{x})} = \left[ \exp\left(i \sum_{1 \le j <k \le n} \phi_{\{j,k\}}(\vec{x})\, Z_j \otimes Z_k\right) \exp\left(i \sum_{j=1}^n \phi_{\{j\}}(\vec{x})\, Z_j \right)  H^{\otimes n} \right]^d \end{equation*} Here, $Z$ denotes the Pauli-$Z$ operator, $n$ denotes the number of qubits (corresponding to the number of features), $d$ is the number of repetitions, and $\phi_S(\vec{x})$ is defined as: \begin{equation*} \phi_{S}(\vec{x}) = \begin{cases} x_i, & S = \{i\} \\ (\pi - x_i) (\pi - x_j), & S = \{i, j\} \end{cases} \end{equation*} With these ingredients, we can construct the quantum kernel as shown in the following equation: \begin{equation*} K(\vec{x}, \vec{y}) = \lvert \langle \Phi(\vec{x}) \vert \Phi(\vec{y}) \rangle \rvert^2  = \langle 0^{\otimes n} \vert \mathcal{U}_{\Phi(\vec{x})}^\dagger \mathcal{U}_{\Phi(\vec{y})} \vert 0^{\otimes n} \rangle\end{equation*} where $ \mathcal{U}_{\Phi(\vec{x})}^\dagger $ denotes the Hermitian adjoint of $ \mathcal{U}_{\Phi(\vec{x})}$ .

Read More

Field Quantization. Annihilation and Creation operators

Taking up the Hamiltonian equation from Field Quantization. Hamiltonian for a single-mode field

\begin{equation} H = \frac{1}{2} \left( p^2 + \omega^2 q^2  \right) \end{equation}

Where $q$ and $p$ are the canonical variables. To make a quantum approach  we just replace them with the respective operator $\hat{q}$ and $\hat{p}$, which must satisfy the canonical commutation relation:

\begin{equation} \left[ \hat{q},\hat{p} \right]=i\hbar \hat{I} \equiv i\hbar \end{equation}

With these operators the Hamiltonian transforms into the operator:

\begin{equation} \hat{H} = \frac{1}{2} \left( \hat{p} ^2 + \omega^2 \hat{q} ^2  \right)  \end{equation}

It is convenient to introduce the non-Hermitian annihilation $\hat{a}$ and creation $\hat{a} ^\dagger$ operators given by:

\begin{equation} \hat{a} = (2 \hbar \omega)^{-1/2} (\omega \hat{q}+ i\hat{p}) \end{equation} \begin{equation} \hat{a} ^\dagger = (2 \hbar \omega)^{-1/2} (\omega \hat{q}- i\hat{p}) \end{equation}

These satisfiy the commutation relation: 

\begin{equation}  \left[ \hat{a},\hat{a} ^\dagger \right] =  \hat{a} \hat{a} ^\dagger -  \hat{a}^\dagger \hat{a}= 1 \end{equation}

Noting that

\begin{align*} \hat{a} ^\dagger \hat{a} &= (2 \hbar \omega)^{-1/2} (\omega \hat{q}- i\hat{p})(2 \hbar \omega)^{-1/2} (\omega \hat{q}+ i\hat{p}) =  \frac{1}{2 \hbar \omega}\left[  \omega^2\hat{q}^2 + i\omega\hat{q}\hat{p}-i\omega\hat{p}\hat{q}+\hat{p}^2  \right] \\ \\ &=  \frac{1}{2 \hbar \omega}\left[  \omega^2\hat{q}^2 + i\omega \left[ \hat{q},\hat{p} \right]+\hat{p}^2  \right] =  \frac{1}{2 \hbar \omega}\left[  \omega^2\hat{q}^2 - \omega\hbar +\hat{p}^2  \right] = \frac{1}{\hbar \omega} \frac{1}{2} \left( \hat{p}^2 +  \omega^2\hat{q}^2 \right)  - \frac{1}{2} \\ \\ &= \frac{1}{\hbar \omega}\hat{H}-\frac{1}{2} \end{align*}

So, the Hamiltonian operator can be defined as:

\begin{equation} \hat{H} = \hbar\omega \left(  \hat{a} ^\dagger \hat{a} + \frac{1}{2} \right) \end{equation}

Now we can describe the energy eigenvalues. We denote $\vert n \rangle$ as energy eigenstate of the single mode field with eigenvalue $E_n$ such that:

\begin{equation} \hat{H}\vert n \rangle =  \hbar\omega \left(  \hat{a} ^\dagger \hat{a} + \frac{1}{2} \right) \vert n \rangle = E_n \vert n \rangle \end{equation}

The operator $\hat{a}^\dagger \hat{a}$ has a great importance and is called number operator $\hat{n}$. We will generate the eigenvalue equations for $\hat{a}^\dagger \vert n \rangle$ and $\hat{a} \vert n \rangle$ to appreciate the effect of the operators in the energy level and understand why they are called that. Multiplying Eq. (8) by  $\hat{a}^\dagger$ we obtain:

\begin{equation*} \hbar\omega \left( \hat{a} ^\dagger \hat{a} ^\dagger \hat{a} + \frac{1}{2}\hat{a} ^\dagger \right) \vert n \rangle =  E_n \hat{a}^\dagger \vert n \rangle \end{equation*}

\begin{equation*} \hbar\omega \left( \hat{a} ^\dagger \left(\hat{a}\hat{a}^\dagger -1 \right) + \frac{1}{2}\hat{a} ^\dagger \right) \vert n \rangle =  E_n \hat{a}^\dagger \vert n \rangle \end{equation*}

\begin{equation*} \hbar\omega \left( \hat{a} ^\dagger\hat{a}\hat{a}^\dagger + \frac{1}{2}\hat{a} ^\dagger \right) \vert n \rangle =   E_n  \hat{a}^\dagger \vert n \rangle +  \hbar\omega  \hat{a}^\dagger \vert n \rangle \end{equation*}

\begin{equation*} \hbar\omega \left( \hat{a} ^\dagger\hat{a} + \frac{1}{2} \right) \left(\hat{a}^\dagger \vert n \rangle \right)=  \left( E_n + \hbar\omega \right) \left( \hat{a}^\dagger \vert n \rangle \right) \end{equation*}

\begin{equation} \Rightarrow \hat{H} \left(\hat{a}^\dagger \vert n \rangle \right)=  \left( E_n + \hbar\omega \right) \left( \hat{a}^\dagger \vert n \rangle \right) \end{equation}

This is the equation for the eigenstate  $\hat{a}^\dagger \vert n \rangle$, it has energy eigenvalue of $E_n + \hbar \omega$. We can interpret this as if the operator $\hat{a}^\dagger$ created one quantum of energy $\hbar \omega$, that is why it is called as the creation operator. In the same way, we can multiply Eq. (8) by $\hat{a}$ to obtain the equation for the eigenstate $\hat{a}\vert n \rangle$:

\begin{equation} \hat{H} \left(\hat{a} \vert n \rangle \right)=  \left( E_n - \hbar\omega \right) \left( \hat{a} \vert n \rangle \right) \end{equation}

Similar to the previous case, we can interpret it as if the operator $\hat{a}$ eliminated or annihilated one quantum of energy $\hbar \omega$, that is why it is called as the annihilation operator. 

For the states $\hat{a}\vert n \rangle$, $\hat{a}^\dagger \vert n \rangle$ and $\hat{n} \vert n \rangle$ we have:

\begin{equation}\hat{a}\vert n \rangle = c_n \vert n-1 \rangle \end{equation}

\begin{equation}\hat{a}^\dagger \vert n \rangle = d_n \vert n+1 \rangle \end{equation}

\begin{equation}\hat{n} \vert n \rangle = n \vert n \rangle \end{equation}

Where $c_n$ and $d_n$ are constants. The number of states must be normalized, i.e. $\langle n \vert n \rangle = 1$. The inner product of  $\hat{a}\vert n \rangle$ with itself is:

\begin{equation} (\langle n \vert \hat{a}^\dagger)(\hat{a}\vert n \rangle) = \langle n \vert \hat{a}^\dagger \hat{a} \vert n \rangle = \langle n \vert \hat{n} \vert n \rangle = n \langle n \vert n \rangle = n \end{equation}

Also

\begin{equation} (\langle n \vert \hat{a}^\dagger)(\hat{a}\vert n \rangle) = \langle n-1 \vert c_n^* c_n  \vert n-1 \rangle = \vert c_n \vert ^2 \langle n-1 \vert n-1 \rangle = \vert c_n \vert ^2 \end{equation}

Thus $c_n = \sqrt{n}$ and

\begin{equation} \boxed{ \hat{a}\vert n \rangle = \sqrt{n} \vert n-1 \rangle} \end{equation}

In the same way, the inner product of  $\hat{a}^\dagger \vert n \rangle$ with itself is:

\begin{equation} (\langle n \vert \hat{a})(\hat{a}^\dagger \vert n \rangle) = \langle n \vert \hat{a} \hat{a}^\dagger \vert n \rangle = \langle n \vert (\hat{a}^\dagger\hat{a}+1) \vert n \rangle = \langle n \vert \hat{n} \vert n \rangle +  \langle n \vert  n \rangle =  n + 1\end{equation}

Also

\begin{equation} (\langle n \vert \hat{a})(\hat{a}^\dagger \vert n \rangle) = \langle n+1 \vert d_n^* d_n \vert n+1 \rangle = \vert d_n \vert ^2 \langle n+1 \vert n+1 \rangle = \vert d_n \vert ^2 \end{equation}

Thus $d_n = \sqrt{n+1}$ and

\begin{equation}\boxed{ \hat{a}^\dagger \vert n \rangle = \sqrt{n+1} \vert n+1 \rangle} \end{equation}

Read More

Field Quantization. Hamiltonian for a single-mode field

We have the case of a radiant field confined in one dimensional cavity along the z-axis with perfectly conducting walls at  $z = 0$ and $z = L$, so that the electric field vanish in the boundaries as shown in:

Maxwell's equations without sources are:

\begin{equation} \nabla \times \textbf{E} = \frac{\partial \textbf{B}}{\partial t}  \end{equation}

\begin{equation} \nabla \times \textbf{B} = \mu_0 \varepsilon_0 \frac{\partial \textbf{E}}{\partial t}  \end{equation}

\begin{equation} \nabla \cdot \textbf{B} = 0  \end{equation}

\begin{equation}  \nabla \cdot \textbf{E} = 0  \end{equation}

The field is polarized in x-direction, i.e. $\textbf{E}(\textbf{r},t) = \mathbf{e}_x  E_x(z,t)$, with $\textbf{e}_x $ an unit polarization vector. A field that satisfies Maxwell's equations and boundary conditions is:

\begin{equation} E_x(z,t)=\left( \frac{2\omega^{2}}{V\varepsilon_0} \right)^{1/2}q(t) \text{sin}(kz)  \end{equation}

With $\omega$ the frequency of the mode, $k=\cfrac{\omega}{c}$ the wave number, $V$ the effective volume of the cavity and $q(t)$ the canonical position. We can not have all frequencies due to the boundary condition at $z=L$, this only allowed frequencies $\omega_m = c \cfrac{m\pi}{L}, \quad m=1,2,\cdots$. From Eq. (2) and Eq. (5) we obtain: 

\begin{equation*} \textbf{e}_x \left( \partial_y B_z - \partial_z B_y  \right) + \textbf{e}_y \left( \partial_z B_x - \partial_x B_z  \right) + \textbf{e}_z \left( \partial_x B_y - \partial_y B_x  \right) = \textbf{e}_x \left( \mu_0\varepsilon_0 \partial_t E_x \right) \\ \partial_y B_z - \partial_z B_y = \mu_0\varepsilon_0 \left( \frac{2\omega^{2}}{V\varepsilon_0} \right)^{1/2} \text{sin}(kz) \partial_t q =  \mu_0\varepsilon_0 \left( \frac{2\omega^{2}}{V\varepsilon_0} \right)^{1/2} \dot{q}(t) \text{sin}(kz)  \\  - \partial_z B_y = \mu_0\varepsilon_0 \left( \frac{2\omega^{2}}{V\varepsilon_0} \right)^{1/2} \dot{q}(t) \text{sin}(kz) \end{equation*}

\begin{equation} \Rightarrow  B_y (z,t) = \frac{\mu_0\varepsilon_0}{k} \left( \frac{2\omega^{2}}{V\varepsilon_0} \right)^{1/2} \dot{q}(t) \text{cos}(kz) \end{equation}

The Hamiltonian of the field described above is:

\begin{equation} H=\frac{1}{2}\int dV \left[ \varepsilon_0 E_x^{2}(z,t) + \frac{1}{\mu_0}B_y^{2}(z,t) \right] \end{equation}

Substituting Eq. (5) and Eq. (6) in Eq. (7):

\begin{equation*} H=\frac{1}{2} \left[  \varepsilon_0 \frac{2\omega^{2}}{V\varepsilon_0} q^2(t) \int dV \text{sin}^2(kz)  + \frac{1}{\mu_0} \frac{\mu_0^2 \varepsilon_0^2}{k^2} \frac{2\omega^{2}}{V\varepsilon_0} \dot{q}^2(t) \int dV \text{cos}^2(kz) \right] \end{equation*}

It is important to emphasize that $V$ in the equations for $E_x$ and $B_y$ is the volume of the cavity, i.e. it is a constant. Noting that $k=\cfrac{\omega}{c}$ and $\mu_0\varepsilon_0 = \cfrac{1}{c^2}$

\begin{equation*} H=\frac{1}{2} \left[  \frac{2\omega^{2}}{V} q^2(t) \int dV \text{sin}^2(kz)  +   \frac{2}{V} \dot{q}^2(t) \int dV \text{cos}^2(kz) \right] \end{equation*}

For this case we have $\int dV = A\int_L dz$, so:

\begin{align*} H &= \frac{1}{2}A \left[  \frac{2\omega^{2}}{V} q^2(t) \int_L dz \; \text{sin}^2(kz)  +   \frac{2}{V} \dot{q}^2(t) \int_L dz \; \text{cos}^2(kz) \right] \\ \\ &= \frac{1}{2}A \left[ \frac{\omega^2 q^2(t)L}{V} +  \frac{\dot{q}^2(t) L}{V}  \right]\end{align*}

Considering a particle of unit mass, i.e. the canonical momentum is $p(t) = \dot{q}(t)$ and noting that $V=AL$, the Hamiltonian results:

\begin{equation} \boxed{H = \frac{1}{2} \left( p^2 + \omega^2 q^2  \right)} \end{equation}

Read More

Bra-Ket (Dirac) Notation

In quantum mechanics, we can describe pure quantum states using an n-dimensional vector (also called a rank-1 tensor). This vector is written in Dirac notation as a ket and represents the complete information of the state: $$  \vert \Psi  \rangle  =  \begin{pmatrix} \alpha_1 \\ \vdots \\ \alpha_n \end{pmatrix} $$

Each component $\alpha_i$ is a complex number that encodes both amplitude and phase. Physically, the squared magnitude $|\alpha_i|^2$ gives the probability of finding the system in the corresponding basis state when a measurement is performed.

From this ket we can construct the corresponding bra, which belongs to the dual space. It is obtained by transposing the ket and taking the complex conjugate of every component: $$  \langle \Psi  \vert  =  \begin{pmatrix} \alpha_1^* & \cdots & \alpha_n^*  \end{pmatrix} $$ At first instance we can define some products using bras and kets, the inner product, outer product and tensor product.

Inner product

The inner product (or scalar product) combines a bra with a ket and yields a single complex number:  \begin{equation*} \langle \Psi  \vert \Psi  \rangle  =  \begin{pmatrix} \alpha_1^* & \cdots & \alpha_n^* \end{pmatrix} \begin{pmatrix} \alpha_1 \\ \vdots \\ \alpha_n \end{pmatrix} =  \alpha_1^*  \alpha_1 + \cdots \alpha_n^*  \alpha_n =  \vert \alpha_1 \vert ^2 + \cdots + \vert \alpha_n \vert ^2  \end{equation*}   

This corresponds to the squared norm of the state. For physical states, this value must equal 1, reflecting the fact that the total probability across all possible outcomes is always conserved.

Outer product

The outer product combines a ket with its corresponding bra, producing a matrix instead of a number: \begin{align*} \vert  \Psi \rangle \langle  \Psi  \vert  &=   \begin{pmatrix} \alpha_1 \\ \vdots \\ \alpha_n \end{pmatrix} \begin{pmatrix} \alpha_1^* & \cdots & \alpha_n^* \end{pmatrix} =  \begin{pmatrix}  \alpha_1  \alpha_1^* &  \alpha_1  \alpha_2^*  & \cdots &  \alpha_1  \alpha_n^* \\  \alpha_2  \alpha_1^* &  \alpha_2  \alpha_2^*  & \cdots &  \alpha_2  \alpha_n^* \\ \vdots & \vdots & \ddots & \vdots \\  \alpha_n  \alpha_1^* &  \alpha_n  \alpha_2^*  & \cdots &  \alpha_n  \alpha_n^* \end{pmatrix} \\ \\  &=   \begin{pmatrix}  \vert \alpha_1 \vert ^2 &  \alpha_1  \alpha_2^*  & \cdots &  \alpha_1  \alpha_n^* \\  \alpha_2  \alpha_1^* &  \vert \alpha_2 \vert ^2  & \cdots &  \alpha_2  \alpha_n^* \\ \vdots & \vdots & \ddots & \vdots \\  \alpha_n  \alpha_1^* &  \alpha_n  \alpha_2^*  & \cdots & \vert \alpha_n \vert ^2  \end{pmatrix} \end{align*}

This operator is fundamental in quantum mechanics. For example, it is used to represent projectors onto states and to build density matrices, which describe both pure and mixed states in quantum theory.

Tensor product

Finally, the tensor product (or Kronecker product) is the operation that allows us to combine two independent quantum systems into a larger one: $ \vert \alpha \rangle \otimes \vert \beta \rangle \equiv \vert \alpha \rangle \vert \beta \rangle \equiv  \vert \alpha , \beta \rangle \equiv  \vert \alpha \beta \rangle $. 

Supposing 2-dimensional kets $ \vert \alpha \rangle = \big(\begin{smallmatrix} \alpha_1 \\ \alpha_2 \end{smallmatrix}\big) $ and $\vert \beta \rangle = \big(\begin{smallmatrix} \beta_1 \\ \beta_2 \end{smallmatrix}\big) $ we can define the tensor product as:

\begin{align*} \vert \alpha \rangle \otimes \vert \beta \rangle  &=   \begin{pmatrix} \alpha_1 \\ \alpha_2 \end{pmatrix} \otimes \begin{pmatrix} \beta_1 \\ \beta_2 \end{pmatrix} =  \begin{pmatrix} \alpha_1 \begin{pmatrix} \beta_1 \\ \beta_2  \end{pmatrix} \\ \alpha_2  \begin{pmatrix} \beta_1 \\ \beta_2  \end{pmatrix} \end{pmatrix} = \begin{pmatrix} \alpha_1 \beta_1 \\  \alpha_1 \beta_2  \\  \alpha_2 \beta_1 \\  \alpha_2 \beta_2  \end{pmatrix}  \end{align*} 

The dimension of the resulting vector is the product of the dimensions of the original ones. This operation is the mathematical foundation for describing multi-particle systems and quantum entanglement.

Read More

Intensity Transformations (Part 2)

Welcome back to our exploration of Intensity Transformations. This post is a continuation of our previous discussion, where we covered the general introduction, some auxiliary functions, Gamma Transformation, and Log Transformation. If you haven't read the first part yet, I highly recommend you start here to understand the foundational concepts. In this post, we focus on the Contrast-Stretching and Threshold transformations.

Contrast-Stretching Transformations

As the name suggests, the Contrast-Stretching technique aims to enhance the contrast in an image by stretching its intensity values to span the entire dynamic range. It expands a narrow range of input levels into a wide (stretched) range of output levels, resulting in an image with higher contrast. 

The commonly used formula for the Contrast-Stretching Transformation is:

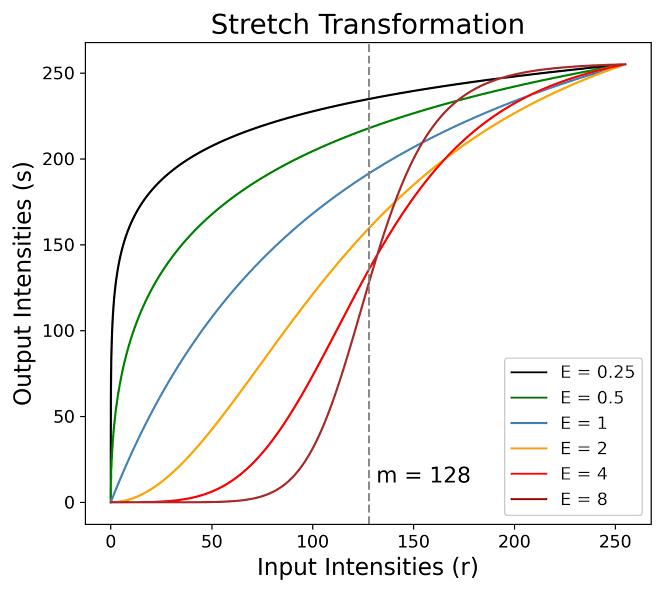
\begin{equation*} s = \frac{1}{1 + \left( \dfrac{m}{r} \right)^E} \end{equation*}

In this equation, $m$ denotates the intensity value around which the stretching is centered, and $E$ controls the slope of the function. Below is a graphical representation of the curves generated using different values of $E$:

These curves illustrate how varying $E$ affects the contrast-stretching process. A higher value of $E$ results in a steeper curve, leading to more pronounced contrast enhancement around the intensity level $m$, darkening the intensity levels below $m$ and brightening the levels above it.

Python Implementation

We now introduce a practical implementation with the stretch_transformation function. This function applies the stretch transformation to an image, enhancing its contrast by expanding the intensity values.

# Function to apply the Stretch Transformation
def stretch_transformation(Img, m = 128, E = 4):
    # Apply the Stretch transformation formula
    s = 1 / (1 + (m / Img)**E )
    # Scale the transformed image to the range of 0-255 and convert to uint8
    Img_transformed = np.array(scaling(s, 0, 255), dtype = np.uint8)
    return Img_transformed

The function first applies the Stretch Transformation formula to the input image. After the transformation, it employs the scaling function to scale the transformed pixel values back to the range of 0-255. Finally, the transformed image is converted to an 8-bit unsigned integer format (np.uint8).

Having explored the concept of Contrast-Stretching transformations, we can apply this technique to a real image using the following code:

# Load an image in grayscale
Im3 = cv2.imread('/content/Image_3.png', cv2.IMREAD_GRAYSCALE)
# Apply the Stretch transformation
Im3_transformed = stretch_transformation(Im3, m = 60, E = 1)

# Prepare images for display
images = [Im3, Im3_transformed]
titles = ['Original Image', 'Stretching Transformation']
# Use the plot_images function to display the original and transformed images
plot_images(images, titles, 1, 2, (10, 7))

We first load an image in grayscale from a specified path (/content/Image_3.png). We then apply the Stretch Transformation with a midpoint $m = 60$  and a slope $E = 1$. We finally apply the plot_images function to display the original and transformed images. The results are shown below:

In the original image, the details and bones of the skeleton are discernible only in certain regions. Particularly, the lower and upper extremities are barely visible, obscured by the limited contrast of the image. However, the transformed image presents a stark contrast. The details are noticeably more visible. This enhanced visibility is a direct result of the stretching transformation, which has effectively expanded the range of intensity values.

Threshold Transformations

Thresholding is the simplest yet effective method for segmenting images. It involves converting an image from color or grayscale to a binary format, essentially reducing it to just two colors: black and white.

This technique is most commonly used to isolate areas of interest within an image, effectively ignoring the parts that are not relevant to the specific task. It's particularly useful in applications where the distinction between objects and the background is crucial.

In the simplest form of thresholding, each pixel in an image is compared to a predefined threshold value $T$. If the intensity $f(x,y)$ of a pixel is less than $T$, that pixel is turned black (0 value).  Conversely, if a pixel's intensity is greater than $T$, it is turned white (255 value). This binary transformation creates a clear distinction between higher and lower intensity values, simplifying the image's content for further analysis or processing.

Python Implementation

Having discussed the concept of threshold transformations, we now apply this technique to a real image using the following code:

# Load an image in grayscale
Im3 = cv2.imread('/content/Image_3.png', cv2.IMREAD_GRAYSCALE)
# Apply the Threshold transformation
_ , Im3_threshold = cv2.threshold(Im3, 25, Im3.max(), cv2.THRESH_BINARY)

# Prepare images for display
images = [Im3, Im3_threshold]
titles = ['Original Image', 'Threshold Transformation']
# Use the plot_images function to display the original and transformed images
plot_images(images, titles, 1, 2, (10, 7))

We first load an image in grayscale from a specified path (/content/Image_3.png). We then apply the threshold transformation using OpenCV's threshold function, the threshold value is set to $25$, and the maximum value to Im3.max(). This means that all pixel values below $25$ are set to $0$ (black), and those above $25$ are set to the maximum pixel value of the image (white). Finally, we apply the plot_images function to display the original and transformed images. The results are shown below:

The original image is the same as in the previous section, but now the transformation has been performed using a threshold function. This resulted in a binary image that represents the skeleton. However, it loses information about the extremities and exhibits poor segmentation in the pelvic and rib areas.

Bonus: Adaptive Threshold Transformations

Adaptive Threshold Transformation is a sophisticated alternative to the basic thresholding technique. While standard thresholding applies a single threshold value across the entire image, adaptive thresholding adjusts the threshold dynamically over different regions of the image. This approach is particularly effective in dealing with images where lighting conditions vary across different areas, leading to uneven illumination.

Adaptive thresholding works by calculating the threshold for a pixel based on a small region around it, commonly employing statistical measures, such as the mean or median. This means that different parts of the image can have different thresholds, allowing for more nuanced and localized segmentation. The method is especially useful in scenarios where the background brightness or texture varies significantly, posing challenges for global thresholding methods.

Adaptive thresholding is widely used in applications such as text recognition, where it helps to isolate characters from a variable background, or in medical imaging, where it can enhance the visibility of features in areas with differing lighting conditions.

Python Implementation

Having discussed the concept of threshold transformations, we now apply this technique to a real image using the following code:

After discussing the theory behind adaptive threshold transformation, we are ready for the practical implementation. We apply this technique to the same image as the previous threshold transformation with the following code:

# Load an image in grayscale
Im3 = cv2.imread('/content/Image_3.png', cv2.IMREAD_GRAYSCALE)
# Apply the Adaptive Threshold transformation
Im3_adapt_threshold = cv2.adaptiveThreshold(Im3, 255, cv2.ADAPTIVE_THRESH_MEAN_C, cv2.THRESH_BINARY, 61,-2)

# Prepare images for display
images = [Im3, Im3_adapt_threshold]
titles = ['Original Image', 'Adaptive Threshold']
# Use the plot_images function to display the original and transformed images
plot_images(images, titles, 1, 2, (10, 7))

We first load an image in grayscale from a specified path (/content/Image_3.png). Then, we apply the adaptive threshold transformation using OpenCV's adaptiveThreshold function. The parameters include a maximum value of $255$, the adaptive method cv2.ADAPTIVE_THRESH_MEAN_C (which uses the mean of the neighborhood area), the threshold type cv2.THRESH_BINARY, a block size of $61$ (determining the size $61 \times 61$ of the neighborhood area), and a constant of $-2$ subtracted from the mean. Finally, we use the plot_images function to display the original and transformed images side by side. The results are shown below:

Unlike the results obtained with a basic thresholding technique, the adaptive threshold transformation allows for the successful segmentation of the complete skeleton by tuning the method's parameters. This approach results in a more detailed and comprehensive visualization of the skeletal structure. From the extremities to the ribs, pelvis, and skull, each part of the skeleton is clearly delineated.

Read More